Research

Numerical methods for the Ginzburg-Landau equation

Superconductors are materials that allow to conduct electricity without any electrical resistance. The superconductivity in Ω can be modeled by a complex-valued wave function \(u \colon \Omega \to \mathbb{C}\), which is called the order parameter. The physical quantity of interest is \(|u|^2\), which denotes the density of the superconducting electron pairs. Together with the magnetic vector potential \(\mathbf{A}\), the order parameter can be characterized as a minimizer of the Ginzburg–Landau energy

\[E(u,\mathbf{A}) = \frac{1}{2} \int_\Omega |\frac{i}{\kappa} \nabla u + \mathbf{A} u |^2 + \frac{1}{2} \bigl( 1- |u|^2 \bigr)^2 + |\textup{curl} \mathbf{A} - \mathbf{H}|^2 \,dx,\]

where \(\mathbf{H}\) is the applied magnetic field. The size of the parameter \(\kappa\) is crucial for the appearance of vortices. The so-called high-\(\kappa\) regime is the physically most interesting regime, but numerically it is also the most challenging one because it requires fine meshes to resolve all lattice structures. In our research we want to understand how we have to discretize this problem in order to capture the correct vortex patterns.

       
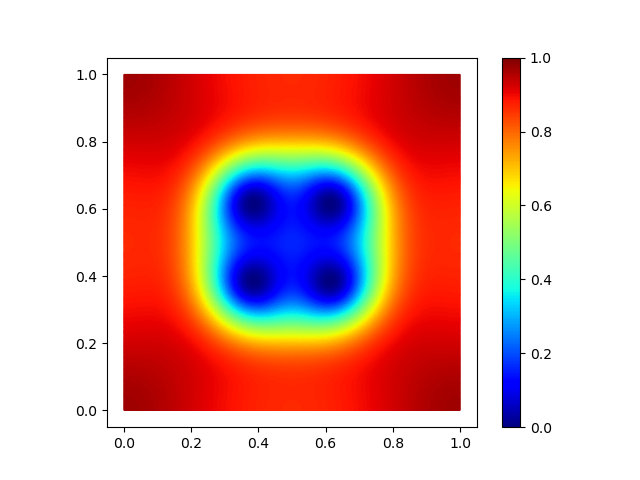
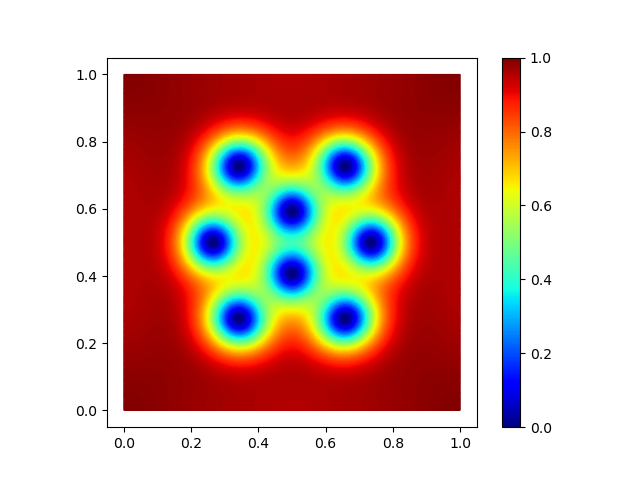
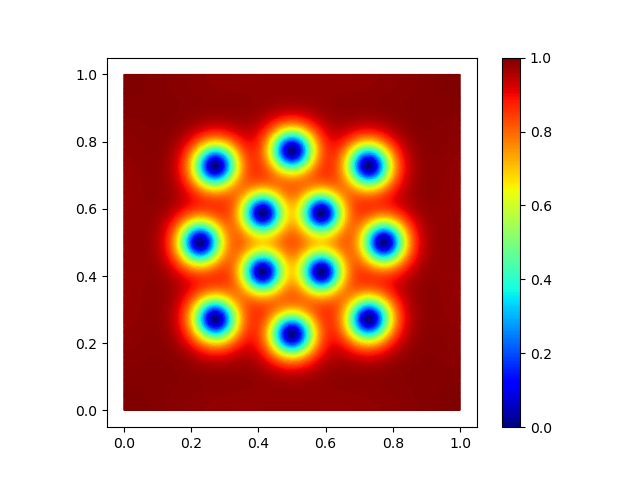
Density $|u|^2$ of minimizers for the different values of \\(\kappa=10,17,24\\).

Numerical methods for nonlinear optics in plasmonic nanogaps

Here, we study (nonlinear) Maxwell equations on a 3d domain which interacts with a 2d materials, such as Graphene and transition-metal dichalcogenides (TMDC). The interaction takes place on the interface \(F_{\small{\textup{int}}}\).

via an interface jump in the tangential component of the magnetic field \(\mathbf{H}\) coming from a surface current. For the current can either be modelled via response theory or as a current derived from a magnetic Schrödinger equation. Because of its interdisciplinary aspects, this project will be conducted together with the Theoretical Optics & Photonics group of K. Busch at HU Berlin.

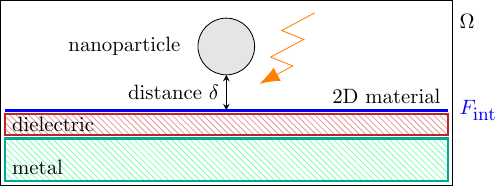
Experimental set-up

Numerical methods for nonlinear wave equations

In this part, we study the time, space and full discretization of various nonlinear wave(-type) equations. These nonlinear effects pose severe challenges in the well-posedness of the problem as well as in the error analysis. Our overall goal is o construct and analyze reliable numerical methods via an interplay of the strategies from the wellposedness result and the restrictions (and advantages) from the finite dimensional subspace.